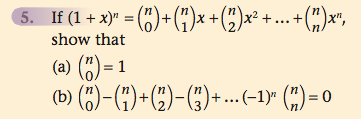High School Mathematics Questions and Answers. Feel free to use the Search bar for this site, just below. The list of Labels in the right hand column below is also useful. Most of the questions on this site are from NSW, Australia curriculum.
Monday, 30 November 2015
Thursday, 26 November 2015
Tuesday, 24 November 2015
GROVE HSC 3U EX2.8 - REGARDING Q15
JUst regarding finding the second derivative of this (good luck to you!)
WOLFRAM ALPHA SAYS
AND THIS CAN NEVER BE ZERO, SO THERE ARE NO INFLEXIONS.
(yes x here should be h)
GROVE HSC 3U - EX2.8 - SIMILAR QUESTION
Question: Find any non horizontal inflexions.
(by finding second derivative)
[this is not Q15, but looks similar.
It's good practice for derivatives]
Monday, 23 November 2015
Sunday, 22 November 2015
GROVE HSC 3U - TEST YOURSELF 10 - Q5
(a) Put $x=0$ on LHS and RHS!
(b) Put $x=-1$ on LHS and RHS!
Keep in mind $(-1)^2=1$, $(-1)^3=-1$, $(-1)^4=1$, ...
Saturday, 21 November 2015
GROVE PRELIM 2U/3U TEST YOURSELF 8 - Q18
$y'=-{1\over 3}x^{-2}$
$y'=-{1\over 3x^2}$
$y'=-{1\over 3\left({1\over 6}\right)^2}=-{36\over 3}=-12$
When $x=1/6$, $y=1/(3(1/6))=2$
$y-2=-12(x-1/6)$
$y-2=-12x+2$
$12x+y-4=0$
JH :-)
GROVE PRELIM 2U/3U TEST YOURSELF 8 - Q20
$y'={vu'-uv' \over v^2}$
$y'={(2x+1)4-(4x-3)2 \over (2x+1)^2}$
Put $x=1$
$y'={(2(1)+1)4-(4(1)-3)2 \over (2(1)+1)^2}$
$y'=\displaystyle{10\over 9}$
When $x=1$, $y=(4-3)/(2+1)=1/3$.
$(1, 1/3)$.
$y-{1\over 3}={10\over 9}(x-1)$
$9y-3=10(x-1)$
$9y-3=10x-10$
$10x-9y-7=0$
When $y=0$,
$10x-7=0$
$x=\displaystyle {7\over 10}$
GROVE PRELIM 2U/3U TEST YOURSELF 8 - Q15
Find $y'$ then sub $x=2$
Use product rule: If $y=u(x)\times v(x)$ where $u,v$ are functions of $x$, then
$$y'=uv'+u'v$$
Here $$u(x)=(3x-1)^3, v(x)=(2x-1)^2$$$y'=(3x-1)^3\times 2(2x-1)\times 2\\+3(3x-1)^2\times 3(2x-1)^2$
$y'=(3(2)-1)^3\times 2(2(2)-1)\times 2\\+3(3(2)-1)^2\times 3(2(2)-1)^2$
$y'=3525$
GROVE PRELIM 2U/3U EX 8.9 - Q8
$y'=2(x+3)^2+2x\times 2(x+3)$
$y'=2(x^2+6x+9)+4x^2+12x$
$y'=2x^2+12x+18+4x^2+12x$
$y'=6x^2+24x+18$
$\therefore 6x^2+24x+18=14$$6x^2+24x+4=0$
$3x^2+12x+2=0$
$x=\displaystyle { -12\pm \sqrt{12^2-4(3)(2)} \over 6}$
$x=\displaystyle { -12\pm \sqrt{120} \over 6}$
$x=\displaystyle { -12\pm 2\sqrt{30} \over 6}$
$x=\displaystyle { -6\pm \sqrt{30} \over 3}$
GROVE PRELIM 2U/3U TEST YOURSELF 8 - Q15
QUESTION:
Find the equation of the tangent to the curve $y=x^2+2x-5$ that is parallel to the line $y=4x-1$.
SOLUTION:
We need to find the $x$ value on the curve at which the tangent has gradient $m=4$
(since the line $y=4x-1$ has gradient $4$)
(since the line $y=4x-1$ has gradient $4$)
Find $y'$.
(since $y'$ is the gradient of the tangent at $x$)
(since $y'$ is the gradient of the tangent at $x$)
$y'=2x+2$
Solve $y'=4$.
$2x+2=4$
$2x=2$
$x=1$
When $x=1$, $y=(1)^2+2(1)-5=-2$
So the point is $(1,-2)$.
Tangent has equation $y-y_1=m(x-x_1)$
$$y--2=4(x-1)$$
$$y+2=4x-4$$
$$4x-y-6=0$$
GROVE PRELIM 2U/3U BOOK - TEST YOURSELF 8 - Q13
Regarding $\pi$ as a constant and differentiating with respect to $x$.
$${dS\over dr}=2\times 4\pi r^{2-1}$$
$${dS\over dr}=8\pi r^{1}$$
$${dS\over dr}=8\pi r$$
C'est fini.
JH
Firstly, the question should read, "find a quadratic equation...." as there are many....
(a)
$(x-4)(x- -7)=0$
$x^2-4x+7x-28=0$
$x^2+3x-28=0$
(b)
$(x-5-\sqrt{7})(x-5+\sqrt{7})=0$
$((x-5)-\sqrt{7})((x-5)+\sqrt{7})=0$
Thin difference of two squares.
$(x-5)^2-\sqrt{7}^2=0\\$
$(x-5)^2-7=0\\$
$x^2-10x+25 -7=0\\$
$x^2-10x+18=0$
$(x-5-\sqrt{7})(x-5+\sqrt{7})=0$
$((x-5)-\sqrt{7})((x-5)+\sqrt{7})=0$
Thin difference of two squares.
$(x-5)^2-\sqrt{7}^2=0\\$
$(x-5)^2-7=0\\$
$x^2-10x+25 -7=0\\$
$x^2-10x+18=0$
GROVE HSC 3U - TEST YOURSELF 9 (APPROX OF ROOTS) - Q6
It's up to you to find to values of $x$ such that the function value changes sign.
It will be easy trial and error. (unlikely in an actual test)
Let's randomly (with a bit of intuition) try $x=0$ and $x=2$!
$f(x)=x^3+3x-7$
$f(0)=-7<0$
$f(2)=2^3+3(2)-7=8+6-7=7>0$
Since $f(0)<0$ and $f(2)>0$, then there is at least one root between $x=0$ and $x=2$.
Now proceed to half the interval 3 times.....
GROVE PRELIM 2U TEST YOURSELF 9 / GROVE PRELIM 3U TEST YOURSELF 10 - Q13
Multiply both sides by $x$.
$\displaystyle 2x=5+{3\over x}$
$\displaystyle 2x\times x=5\times x+{3\over x}\times x$
$$2x^2=5x+3$$
$$2x^2-5x-3=0$$
$$2x^2-6x+1x-3=0$$
$$2x(x-3) + 1(x-3)=0$$
$$(2x+1)(x-3)=0$$
$$\therefore x=-0.5, 3$$
JH2015 :-)
GROVE PRELIM 2U TEST YOURSELF 9 / GROVE PRELIM 3U TEST YOURSELF 10 - Q12
Here you use sum and product of roots formulas:
$\alpha+\beta = -b/a$ and
$\alpha\beta=c/a$
Friday, 20 November 2015
Monday, 16 November 2015
Sunday, 15 November 2015
Saturday, 14 November 2015
Quadratic Identity question
QUESTION:
Write $3x^2+7$ in the form $a(x-2)^2+b(x+3)+c$.
ANSWER:
$3x^2+7=a(x-2)^2+b(x+3)+c$ holds for all $x$.
Best way is to just expand the RHS and then equate coefficients of the powers of $x$ on LHS and RHS.
$3x^2+7=a(x^2-4x+4)+b(x+3)+c$
$3x^2+7=a x^2-4ax+4a+bx+3b+c$
$3x^2+7=a x^2+(b-4a)x+(4a+3b+c)$
Write $3x^2+7$ in the form $a(x-2)^2+b(x+3)+c$.
ANSWER:
$3x^2+7=a(x-2)^2+b(x+3)+c$ holds for all $x$.
Best way is to just expand the RHS and then equate coefficients of the powers of $x$ on LHS and RHS.
$3x^2+7=a(x^2-4x+4)+b(x+3)+c$
$3x^2+7=a x^2-4ax+4a+bx+3b+c$
$3x^2+7=a x^2+(b-4a)x+(4a+3b+c)$
Therefore
- $a=3$ (comparing coefficient of $x^2$ on LHS and RHS)
- $b-4a=0$ since coefft of $x$ on LHS is 0. (there is no $x$ term)
- $4a+3b+c=7$ (Constant terms on LHS and RHS)
So, $b-4(3)=0$.
$b=12$.
Finally, $4(3)+3(12)+c=7$.
So, $c=7-12-36=-41$.
Final answer: $a=3, b=12, c=-41$.
Friday, 13 November 2015
Grove HSC 3U EX 10.4 - Q3, 9, 11c, 15, 16, 18a, 20ac, 21abe -: Binomial Theorem
QUESTIONS: Q3, 9, 11c, 15, 16, 18a, 20ac, 21abe,
Q3 =====================
 | ||
| Fanks Tatiana :-) Q9 =====================
|
Q15 =====================
Q16 =====================
Q18a =====================
 |
Thanks Juliette :-) |
Q20c =====================
This is a second version of this solution.
 |
| Thanks Tat & Ellie
Q20c - version 2-=====================
 
Q21a=====================
Q21b =====================
  
Q21e =====================
|
Subscribe to:
Posts (Atom)