(a) Find the coordinates of any stationary points and determine their nature.
(b) Find the coordinates of any points of inflexion (and verify using a y'' box that concavity changes)
(c) Get the $x$ and $y$ intercepts. (its possible here)
(d) Sketch it!
------------------------------------------------------------------------
Before we begin just find y' and y'' right away, factorise both of them ready for use later!
$y'=3x^2-6x-9$
$y'=3(x^2-2x-3)$
$y'=3(x-3)(x+1)$ (1)
$y''=6x-6$
$y''=6(x-1)$ (2)
(a) For Stat Pts: solve $y'=0$.
$3(x-3)(x+1)=0$ from (1)
$\therefore x=-1, 3 $
For $x=-1, y=(-1)^3-3(-1)^2-9(-1)+27=32$
For $x=3, y=(3)^3-3(3)^2-9(3)+27=0$
Now determine their nature using a $y'$ box for each point.
For $(-1, 32)$.
[REMARK: Instead of a $y'$ box we could use $y''$ to test concavity at each $x$ value, to determine the nature. This works only if $y''\neq 0$.
Since $y''(-1)<0$ it's concave down at $x=-1$, so it's a MAX.
Since $y''(3)>0$ it's concave up at $x=3$, so it's a MIN. ]
(b) For possible inflexion, solve $y''=0$
$6(x-1)=0$,
$\therefore x=1$.
When $x=1$, $y=(1)^3-3(1)^2-9(1)+27=16$
Possible Inflexion is $(1,16)$.
Verify that is an inflexion using $y''$ box.
(c) For $y$ intercept put $x=0$. $\therefore y=27$ For $x$ intercept put $y=0$. $\therefore 0=x^3-3x^2-9x+27$. By inspection we see that $x=-3,3$.
[REMARK: its often the case that you can't easily find the $x$ intercepts. Only do this as necessary or unless asked to do so in the question!]
(d)



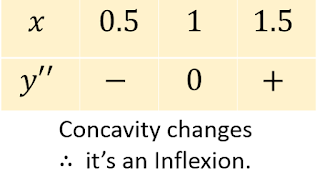

No comments:
Post a Comment