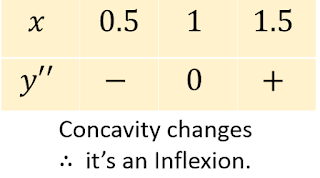High School Mathematics Questions and Answers. Feel free to use the Search bar for this site, just below. The list of Labels in the right hand column below is also useful. Most of the questions on this site are from NSW, Australia curriculum.
Thursday, 29 October 2015
Wednesday, 28 October 2015
GROVE HSC 2U EX 2.9 Q10 - not a stationary point, with asymptotes.
This function goes up to $\infty$ and down to $-\infty$ so it has no maximum or minimum value. (Grove's answer is wrong)
STATIONARY POINTS EXAMPLE WITH AN INFLEXION AS WELL
QUESTION: Consider the curve $$y=x^3-3x^2-9x+27$$
(a) Find the coordinates of any stationary points and determine their nature.
(b) Find the coordinates of any points of inflexion (and verify using a y'' box that concavity changes)
(c) Get the $x$ and $y$ intercepts. (its possible here)
(d) Sketch it!
------------------------------------------------------------------------
Before we begin just find y' and y'' right away, factorise both of them ready for use later!
$y'=3x^2-6x-9$
$y'=3(x^2-2x-3)$
$y'=3(x-3)(x+1)$ (1)
$y''=6x-6$
$y''=6(x-1)$ (2)
(a) For Stat Pts: solve $y'=0$.
$3(x-3)(x+1)=0$ from (1)
$\therefore x=-1, 3 $
For $x=-1, y=(-1)^3-3(-1)^2-9(-1)+27=32$
For $x=3, y=(3)^3-3(3)^2-9(3)+27=0$
Stationary Points are $(-1, 32)$ and $(3,0)$.
Now determine their nature using a $y'$ box for each point.
For $(-1, 32)$.
For $(3, 0)$.
[REMARK: Instead of a $y'$ box we could use $y''$ to test concavity at each $x$ value, to determine the nature. This works only if $y''\neq 0$.
Since $y''(-1)<0$ it's concave down at $x=-1$, so it's a MAX.
Since $y''(3)>0$ it's concave up at $x=3$, so it's a MIN. ]
(b) For possible inflexion, solve $y''=0$
$6(x-1)=0$,
$\therefore x=1$.
When $x=1$, $y=(1)^3-3(1)^2-9(1)+27=16$
Possible Inflexion is $(1,16)$.
Verify that is an inflexion using $y''$ box.
(c) For $y$ intercept put $x=0$. $\therefore y=27$ For $x$ intercept put $y=0$. $\therefore 0=x^3-3x^2-9x+27$. By inspection we see that $x=-3,3$.
[REMARK: its often the case that you can't easily find the $x$ intercepts. Only do this as necessary or unless asked to do so in the question!]
(d)
(a) Find the coordinates of any stationary points and determine their nature.
(b) Find the coordinates of any points of inflexion (and verify using a y'' box that concavity changes)
(c) Get the $x$ and $y$ intercepts. (its possible here)
(d) Sketch it!
------------------------------------------------------------------------
Before we begin just find y' and y'' right away, factorise both of them ready for use later!
$y'=3x^2-6x-9$
$y'=3(x^2-2x-3)$
$y'=3(x-3)(x+1)$ (1)
$y''=6x-6$
$y''=6(x-1)$ (2)
(a) For Stat Pts: solve $y'=0$.
$3(x-3)(x+1)=0$ from (1)
$\therefore x=-1, 3 $
For $x=-1, y=(-1)^3-3(-1)^2-9(-1)+27=32$
For $x=3, y=(3)^3-3(3)^2-9(3)+27=0$
Now determine their nature using a $y'$ box for each point.
For $(-1, 32)$.
Since $y''(-1)<0$ it's concave down at $x=-1$, so it's a MAX.
Since $y''(3)>0$ it's concave up at $x=3$, so it's a MIN. ]
(b) For possible inflexion, solve $y''=0$
$6(x-1)=0$,
$\therefore x=1$.
When $x=1$, $y=(1)^3-3(1)^2-9(1)+27=16$
Possible Inflexion is $(1,16)$.
Verify that is an inflexion using $y''$ box.
(c) For $y$ intercept put $x=0$. $\therefore y=27$ For $x$ intercept put $y=0$. $\therefore 0=x^3-3x^2-9x+27$. By inspection we see that $x=-3,3$.
[REMARK: its often the case that you can't easily find the $x$ intercepts. Only do this as necessary or unless asked to do so in the question!]
(d)
GROVE HSC 2U EX 2.6 Q11 STATIONARY POINT - TRICKY FUNCTION
QUESTION: Find any stationary points on the curve $y=(x-3)\sqrt{4-x}$
This is a product of two functions, so we must use the Product rule to differentiate it.
If $y=uv$, $$y'=vu'+uv'$$
$u=x-3$ $u'=1$
$v=\sqrt{4-x}$
$v=(4-x)^{1\over 2}$
$v'={1\over 2}(4-x)^{-{1\over 2}}(-1)$
$v'=\displaystyle {-1\over 2\sqrt{4-x}}$
[RECALL chain rule. If $y=f(x)^n$, then $$y'=n\,f(x)^{n-1}\times f'(x)$$]
Therefore,
$y'=vu'+uv'$
$y'=\sqrt{4-x} .1 + (x-3)\left( \displaystyle {-1\over 2\sqrt{4-x}}\right)$
$y'=\displaystyle {\sqrt{4-x} \over 1} + \displaystyle{-(x-3) \over 2\sqrt{4-x}}$
This is a product of two functions, so we must use the Product rule to differentiate it.
If $y=uv$, $$y'=vu'+uv'$$
$u=x-3$ $u'=1$
$v=\sqrt{4-x}$
$v=(4-x)^{1\over 2}$
$v'={1\over 2}(4-x)^{-{1\over 2}}(-1)$
$v'=\displaystyle {-1\over 2\sqrt{4-x}}$
[RECALL chain rule. If $y=f(x)^n$, then $$y'=n\,f(x)^{n-1}\times f'(x)$$]
Therefore,
$y'=vu'+uv'$
$y'=\sqrt{4-x} .1 + (x-3)\left( \displaystyle {-1\over 2\sqrt{4-x}}\right)$
$y'=\displaystyle {\sqrt{4-x} \over 1} + \displaystyle{-(x-3) \over 2\sqrt{4-x}}$
$y'=\displaystyle {\sqrt{4-x} \over 1} + \displaystyle{3-x \over 2\sqrt{4-x}}$
[RECALL: $\sqrt{a}\times \sqrt{a}=a$]
$y'=\displaystyle{2(4-x)+3-x \over 2\sqrt{4-x}}$
$y'=\displaystyle {\sqrt{4-x} \over 1}\times {2\sqrt{4-x} \over 2\sqrt{4-x}} + \displaystyle{3-x \over 2\sqrt{4-x}}$
[RECALL: $\sqrt{a}\times \sqrt{a}=a$]
$y'=\displaystyle{8-2x+3-x \over 2\sqrt{4-x}}$
$y'=\displaystyle{11-3x\over 2\sqrt{4-x}}$
FOR STAT POINTS: SOLVE $y'=0$.
$\displaystyle{11-3x\over 2\sqrt{4-x}}=0$
$\therefore 11-3x=0$
$3x=11$
$x=\displaystyle {11\over 3}$
When
$x=\displaystyle {11\over 3}$,
$y=\displaystyle\left({11\over 3}-3\right)\sqrt{4-{11\over 3}}$
$y=\displaystyle{2\over 3}\sqrt{{1\over 3}}$
$y=\displaystyle{2\over 3\sqrt{3}}$
$y=\displaystyle{2\sqrt{3}\over 9}$
$x=\displaystyle {11\over 3}$,
$y=\displaystyle\left({11\over 3}-3\right)\sqrt{4-{11\over 3}}$
$y=\displaystyle{2\over 3}\sqrt{{1\over 3}}$
$y=\displaystyle{2\over 3\sqrt{3}}$
$y=\displaystyle{2\sqrt{3}\over 9}$
Stationary point is $\displaystyle\left({11\over 3},{2\sqrt{3}\over 9}\right)$.
Now determine the nature of this stat point.
So it's a maximum turning point.
Correct to 2 decimal places it's $(3.67, 0.38)$. (Grove gives the answer to 2 d.p. even though the question didn't ask for it)
GROVE HSC 2U EX 2.6 Q5 POINT OF INFLEXION
QUESTION: Show that the curve $f(x)=2x^3-5$ has an inflexion and find its coordinates.
$f'(x)=6x^2$
$f''(x)=12x$
For possible inflexions: solve $f''(x)=0$.
$12x=0$
$\therefore x=0$.
When $x=0, f(0)=2(0)^3-5=-5$.
So, possible inflexion is $(0,-5)$.
Check concavity to verify inflexion.
============================================
PS. the graph wasn't asked for but here it is anyway :-)
$f'(x)=6x^2$
$f''(x)=12x$
For possible inflexions: solve $f''(x)=0$.
$12x=0$
$\therefore x=0$.
When $x=0, f(0)=2(0)^3-5=-5$.
So, possible inflexion is $(0,-5)$.
Check concavity to verify inflexion.
============================================
PS. the graph wasn't asked for but here it is anyway :-)
Tuesday, 27 October 2015
Monday, 26 October 2015
Grove HSC 3U book EX 10.1 Q15 Pascal Triangle identity
Prove $\left({n\atop k}\right)=\left({n-1\atop k-1}\right)+\left({n-1\atop k}\right)$
LHS $=\left({n\atop k}\right)={n!\over k! (n-k)!}$
RHS $=\left( {n-1\atop k-1}\right)+\left({n-1 \atop k}\right)$
$={(n-1)!\over (k-1)! (n-1-(k-1))!}+ {(n-1)!\over k! (n-1-k)!}$
$={(n-1)!\over (k-1)! (n-k)!}+ {(n-1)!\over k! (n-k-1)!}$
$={k(n-1)!\over k(k-1)! (n-k)!}+ {(n-1)!(n-k)\over k! (n-k)(n-k-1)!}$
LHS $=\left({n\atop k}\right)={n!\over k! (n-k)!}$
RHS $=\left( {n-1\atop k-1}\right)+\left({n-1 \atop k}\right)$
$={(n-1)!\over (k-1)! (n-1-(k-1))!}+ {(n-1)!\over k! (n-1-k)!}$
$={(n-1)!\over (k-1)! (n-k)!}+ {(n-1)!\over k! (n-k-1)!}$
$={k(n-1)!\over k(k-1)! (n-k)!}+ {(n-1)!(n-k)\over k! (n-k)(n-k-1)!}$
$={k(n-1)!\over k! (n-k)!}+ {(n-1)!(n-k)\over k! (n-k)!}$
$={k(n-1)! + (n-1)!(n-k)\over k! (n-k)!}$
$={(n-1)!(k + (n-k))\over k! (n-k)!}$
$={(n-1)!n\over k! (n-k)!}$
$={n!\over k! (n-k)!}$
$={(n-1)!(k + (n-k))\over k! (n-k)!}$
$={(n-1)!n\over k! (n-k)!}$
$={n!\over k! (n-k)!}$
=LHS
as required.
Wednesday, 14 October 2015
Thursday, 1 October 2015
Subscribe to:
Posts (Atom)